How Much Does Tax Deferral Save You?

Ever wondered exactly how tax deferral saves you money? Although deferring your income is often cited as a “good thing”, the most common explanation given is a tax arbitrage between your current tax rate and a presumably lower tax rate in retirement. Many people even go so far to say that if your tax rate is the same in retirement then its equivalent, excluding the time value of money. Let’s see if this is actually true.

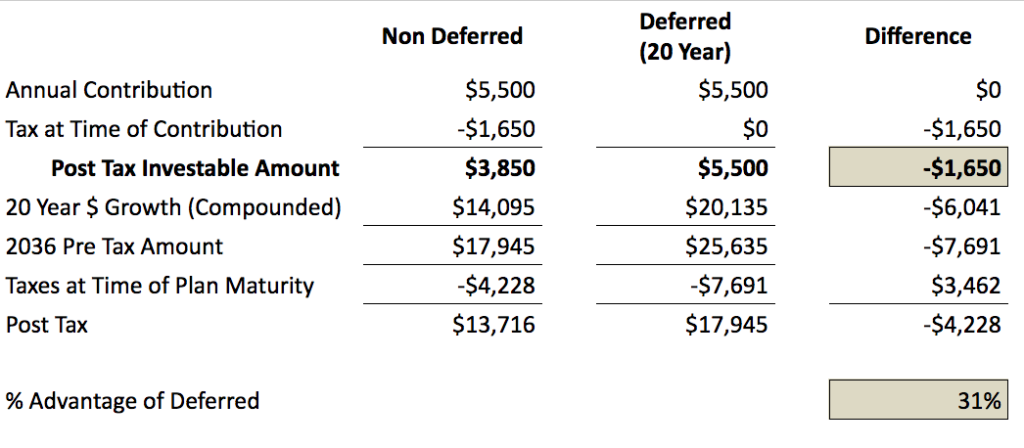
I’ve put together a small scenario which compares a one-time contribution to a deductible Traditional IRA to a standard investment account (non-tax-advantaged) which is then allowed to grow for the next two decades.

Wow! We realized a 31% gain using a tax-deferred investment option given the same tax rate! (30% in this example)

So how does this deferral advantage change with different tax rates, investment returns, and holding periods? We’ll derive the relationships in a moment and show some examples, but you can jump ahead to plug in your own numbers.

Download the Deferral Advantage Estimator
(Go to File > Make a Copy to edit your own)

We can derive a formula for the “Post Tax” amounts shown in the spreadsheet for both the non-deferred and deferred scenarios.

Non-Deferred: Value = P*((1-T)*(1+R)^t – (1-T)*((1+R)^t-1)*T)

Deferred: Value = P*(1+R)^t*(1-T)

Looking at these formulas, you can see the advantage of tax deferral isn’t an arbitrage between current and future tax rates. In fact, we assume the same tax rate T in both formulas. Rearranging a bit highlights the difference:

Non-Deferred: Value = P*(1+R)^t*(1-T) – P*(1-T)*((1+R)^t-1)*T

Deferred: Value = P*(1+R)^t*(1-T)

The first term in both equations is the same! This means the second term in non-deferred (bolded) is entirely responsible for the difference in final values. What is this term? This is the value of the second taxation event. Notice in the spreadsheet above that the non-deferred “2036 Pre Tax Amount” equals the deferred “Post Tax” final value. The non-deferred plan then has an extra taxation event equal to the second term above.

P*(1-T)*((1+R)^t-1)*T

5500*(1-.3)*((1+.08)^20-1)*.3 = $4,228

Absent a tax-arbitrage scenario, the advantage of tax deferral is entirely due to not being taxed twice. Non-deferred investments have a second taxable event whereas tax-deferred investments get to “skip” the first tax treatment. As long as your taxes are no higher in retirement, you will still have an advantage to deferring taxes.

If interested, you could re-do these derivations with separate current and future tax rates. From there, you should be able to identify the “breaking point” for the future tax rate to remove any advantage for tax deferral and then determine how probable you think it is for your personal tax rate to exceed the breaking point rate in the future.

Next we want to be able to calculate the deferral advantage. Deriving the formula from the spreadsheet and simplifying, it is

-(T*((1+R)^t-1)) / ((T-1)*(1+R)^t-T)

Notice that the deferral advantage is independent of the amount of capital invested! It depends only on the tax rate, return rate, and holding period. We can confirm this formula using the above scenario:

-(30%*(1.08^20-1)) / ((30%-1)*(1.08)^20 – 30%) = 31%

Now we can look at the advantage of tax deferral for various tax rates and return rates over different holding periods.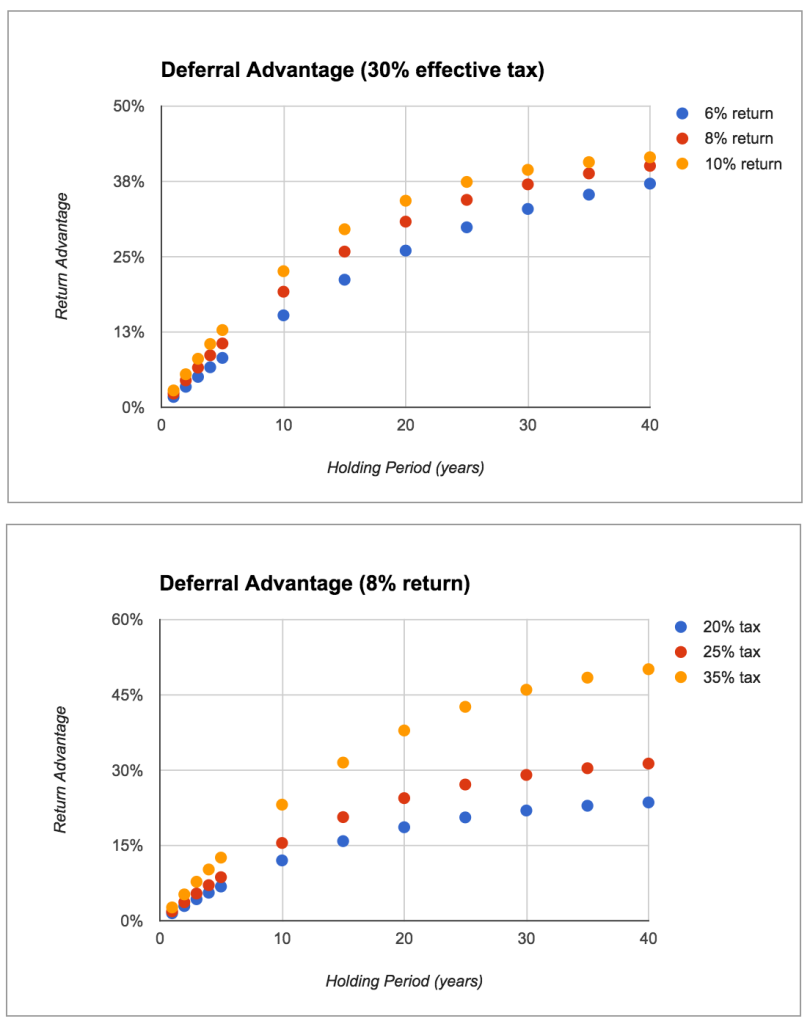

As we can see, the advantage increases with a longer the holding period, improved investment returns, and higher tax rate. Notice that in the best cases (35% tax rate held for 40 years) we can achieve a 50% deferral return advantage! With a 5-year holding period, you see an 11% advantage, which is still nothing to sneeze at.

So what do you do with this information? It can be used in a tax-efficient asset placement strategy to locate potential higher returning, less liquid assets within a tax-deferred account. Be sure to consult your accountant, as losses in tax-advantaged accounts may not be eligible to be carried forward.